Back to Home
Page of CD3WD Project or Back to list of CD3WD Publications
Home
Previous File Next File
(EAH) , y
muestra como los datos que se obtienen de este
ensayo pueden
ser usados para juzgar el rendimiento de una
estufa en
ensayos reales de cocina. En la parte superior
de la tabla
se encuentra irformacion de Ensayos de Agua Hir
viendo
correspondientes a dos modelos de estufa. En la
parte
inferior, esa informacion es aplicada a dos situaciones
imaginarias
de cocina. En el primer ensayo, 4 Kg.
de comida son
calentados hasta ebullicion y luego son cocinados
fuego lento
durante 90 minutos. En el segundo
ensayo se
repite la operacion exactamente, con la excepcion
de que el
cocinado a fuego lento se reduce a 15 minutos.
La cantidad
de comida cocinada viene expresada por:
A' = 4 kg.
La
evaporacion esperada de agua, [A.sub.e] , se calcula a partir
de la razon
de evaporacion en el Ensayo de Agua Hirviendo
de la
duracion del ensayo de cocinado.
La comida y
agua inicialmente usada viene dada por:
A' + [A.sub.e] = A
El tiempo
para llegar a ebullicion, se espera que sea aproximadamente
proporcional
a la comida y agua iniciales
[(Tiempo para
hervir).sub.cocina] =
comida y
agua inicial (ECC)
[(tiempo para
hervir).sub.EAH] x
---------------------------
agua
inicial (EAH)
* El consumo
esperado de madera es la suma de:
- lena usada para hervir: [P.sub.max] x
tiempo para hervir
- lena usada en fuego lento: [P.sub.min] x
tiempo de cocinado a
fuego lento
* El consumo
especifico esperado se obtiene de:
C E = lena para hervir + lena para cocinado
a fuego lento
---------------------------------------------------
agua evaporada, olla #1
El enfoque
anterior, ofrece un estimado, no una garantia.
El Consumo de
lena podra ser mayor que la mostrada debido a
una
flexibilidad dinamica limitada, a un control pobre de
la estufa o a
otras razones,
APENDICE II
Interpretando los
Resultados del Ensayo
La serie de
Ensayos del Agua Hirviendo, Controlado de Cocina o,
del
Rendimiento de Cocina, ofrecen muchas medidas de los mismos
parametros.
Con el fin de obtener la mayor informacion e
introspeccion
de estos
ensayos, resulta util realizar unos pocos y relativamente
sencillos
calculos estadisticos.
El primer
calculo a hacer a partir de un numero de ensayos, como
los de cosumo
especifico de combustible, consumo especifico
estandard,
etc., es el promedio o media aritmetica.
La media
aritmetica
del parametro X de n valores, viene dado por:
(1)
edsxeq1.gif (180x540)
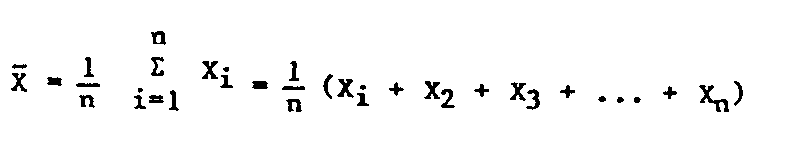
El segundo
estadistico de importancia que debe calcular es la
desviacion
estandard. Esta caracteriza a la
variabilidad entre
las diferentes
pruebas para un mismo parametro. La
desviacion
estandard
viene dada como:
(2)
edsxeq2.gif (162x486)

El cociente
de la desviacion estandard y la media, da como resultado
a un
parametro conocido como el Coeficiente de Variacion
(CDV).
El CDV es una medida normalizada de la
variabilidad la
cual, es
independiente de las unidades de la cantidad siendo
medida.
(3)
edsxeq3.gif (130x393)
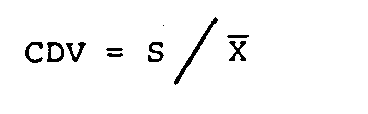
El calculo de
la media, la desviacion estandard y del CDV, debiera
ser aplicado
a ensayos de series individuales en los que,
el CEE, CED,
el PCU, etc., estan siendo determinados, lo mismo
se aplica a
los ensayos de cocinado y cocina donde la diferencia
en consumo de
combustible o CED entre dos diferentes tipos de
estufa o
condiciones de operacion estan siendo estudiados.
En
el ultimo
caso, el parametro de ensayo es primero promediado
para cada
nucleo familiar/cocina (en caso de que se esten realizando
ensayos
multiples para cada cocinero), y posteriormente
promediados
entre nucleos familiares/cocineros para determinar
el promedio
total de uso o de ahorro. El valor
medio de una
cantidad se
puede estimar mas precisamente conforme se practiquen
mas medidas
de la cantidad involucrada. El error
estandard
de la media
calculada, corresponde a la precision con la
cual
realizamos este estimado.
(4)
edsxeq4.gif (130x393)

donde n es el
numero de medidas y S es la desviacion estandard.
Existe un 95%
de probabilidades de que la media real caiga dentro
del rango de
[+ or -] del valor de la media estimada (ver ejemplo
abajo).
La variabilidad puede ser evaluada dentro
del nucleo
familiar o,
entre varios nucleos familiares.
La tabla IV,
muestra los resultados de un conjunto de Ensayos de
Rendimiento
de Cocina, en los que se compara el sistema de fuego
abierto o de
"tres piedras" y de estufas de lena disenadas por
un voluntario
del Cuerpo de Paz, en Kaya, Upper Volta (Hooper,
1980).
Las pruebas realizadas sobre la base de una comida,
fueron
llevadas a
cabo por voluntarios del Cuerpo de Paz (Schroeder,
1981).
El consumo de combustible por comida, fue
evaluado en
seis nucleos
familiares, con un total de 9 a 13 ensayos realizados
por cada
casa.
TABLA IV
Datos del Monitoreo del Rendimiento
de Cocina a partir de
una Serie de Ensayos con Fuego
Abierto y estufas
tipo
"Kaya"
Nucleo
Tamano del
Lena usada por comida
Ahorro de lena de
Familiar
Nucleo
(kg) (*)
la estufa "Kaya" en
relacion al fuego abierto.
fuego
estufa
(kg/
abierto
"Kaya"
comida)
%
1
12
3.72 (5)
3.00
(4) 0.72
19
edsxeq5.gif (117x437)

2
6
3.69 (7)
2.84
(5) 0.85
23
3
8
2.58 (6)
1.88
(6) 0.70
27
edsxeq6.gif (126x475)
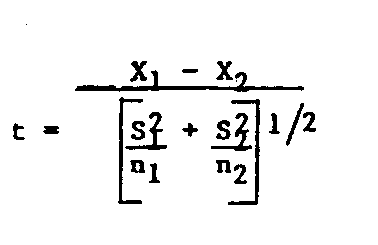
4
14
4.45 (4)
3.05
(6) 1.40
31
5
6 3.82
(6)
2.13 (7)
1.69
44
6
10
3.10 (4)
2.42
(6) 0.68
22
3.56 (32)
2.55 (34)
1.01 28
(*) Los
numeros entre parentesis se refieren al numero de comidas
sobre las cuales se promedio el consumo de
lena (combustible).
Los
resultados de las pruebas dentro de cada nucleo familiar para
cada estufa
en particular, son primero promediados como se
muestra en la
tabla. Luego, el acto de promediar
todos los nucleos
familiares,
se realiza con el fin de calcular los ahorros
totales en
promedio de lena. En este ejemplo, el
ahorro promedio
es de 1.01
kg/comida, o si se quiere, el 28% del consumo de
lena en un
fuego abierto.
Un alto grado
de variabilidad entre los ensayos (es decir, para
CDV mayores
del 30%), indican que existen uno o mas factores que
no fueron
controlados en el desarrollo de las pruebas y que influyeron
grandemente
en los resultados. En nucleos
familiares
donde se
desarrollen Ensayos del Rendimiento de Cocina, se esperan
altos niveles
de variabilidad, pero esto no deberia ocurrir
en pruebas de
laboratorio realizadas con un estricto control.
El promedio y
la desviacion estandard pueden ser usados para
calcular
intervalos de confianza. Asumiendo que
los resultados
de una serie
de calculos del mismo parametro estan normalmente
distribuidos,
el intervalo de confianza del 95% estara dado por:
(5)
Esto
significa que las probabilidades de que el parametro que
se mida se
encuentre entre [bar]X - 2S y [bar]X + 2S es del 95%.
La
comparacion del consumo de lena, CCE, eficiencia, etc., entre
dos
diferentes tipos de estufa, o condiciones de operacion es una
prueba comun
y objetiva. La prueba "t" de
Student se usa para
determinar si
el parametro de ensayo es significativamente diferente
para diversos
tipos de estufa o condiciones de operacion,
asi como la
significancia de cada diferencia. A fin
de efectuar
la prueba
"t", deben calcularse la media y la desviacion estandard
de cada grupo
de pruebas. Luego, el valor de
"t" puede calcularse
asi:
(6)
donde los
subindices 1 y 2 se refieren a cada estufa o, a cada
condicion de
operacion. [bar]X, S, y n, correponden
a los valores
del promedio,
la desviacion estandard y al numero de ensayos
respectivamente
y para cada situacion.
El valor
calculado de "t", es luego comparado con los valores de
"t"
dados en una tabla para determinar si la media de un grupo
es
significativamente mayor que la media del otro.
A continuacion,
encontrara
una tabla resumida con valores de "t".
Los valores
de la tabla
estan listados como una funcion de los "grados
de
libertad" y el nivel de significancia.
Los grados de libertad
representan
simplemente el numero de medidas de prueba, menos
el numero de
parametros que han sido estimados sobre la base de
las
mediciones.
TABLA V
Tabla T
Grados de
Nivel de significancia [infinity]
(%) (*)
libertad
10
5 2.5
1
0.5
1
3.08 6.31
12.70
31.80 63.70
2
1.89 2.92
4.30
6.98
9.92
3
1.64 2.35
3.18
4.54 5.84
4
1.53 2.13
2.78
3.75 4.60
5
1.48 2.01
2.57
3.36 4.03
6
1.44 1.94
2.45
3.14 3.71
7
1.42 1.90
2.36
3.00 3.50
8
1.40 1.86
2.31
2.90 3.36
9
1.38 1.83
2.26
2.82 3.25
10
1.37
1.81
2.23 2.76
3.17
11
1.36 1.80
2.20
2.72 3.11
12
1.36 2.78
2.18
2.68 3.06
13
1.35 1.77
2.16
2.65 3.01
14
1.34 1.76
2.14
2.62 2.98
15
1.34 1.75
2.13
2.60 2.95
16
1.34 1.75
2.12
2.58 2.92
17
1.33 1.74
2.11
2.57 2.90
18
1.33 1.73
2.10
2.55 2.88
19
1.33 1.73
2.09
2.54 2.86
20
1.32 1.72
2.09
2.53 2.84
21
1.32 1.72
2.08
2.52 2.83
22
1.32 1.72
2.07
2.51 2.82
23
1.32 1.71
2.07
2.50 2.81
24
1.32 1.71
2.06
2.49 2.80
25 1.32
1.71
2.06 2.48
2.79
26
1.32 1.70
2.06
2.48 2.78
27
1.31 1.70
2.05
2.47 2.77
28
1.31 1.70
2.05
2.47
2.76
29
1.31 1.70
2.04
2.46 2.76
30
1.31 1.70
2.04
2.46 2.75
[infinity] 1.28
1.64
1.96 2.33
2.58
(*) Este es
el nivel de significancia de un lado que se aplica
para probar
si la media de una poblacion es mayor que la media
de otra.
En este caso:
Grados de Libertad = [n.sub.1]
+ [n.sub.2] - 2
El nivel de
significancia es el porcentaje de probabilidad de
que el resultado
que indica la prueba "t", sea falso.
De alli
que, la
diferencia estadistica entre medias, a partir de los
dos grupos,
se incremente conforme disminuya el nivel de significancia.
La tabla para
la prueba "t", se usa comparando los valores de
"t"
calculados con los de la tabla, usando los grados de libertad
apropiados.
Se puede decir que la media de un grupo de
pruebas es
mayor que otro, a un cierto nivel de significancia
si, el valor
calculado de "t" es mayor que la cifra que aparece
en la tabla a
ese nivel.
La prueba
"t" se puede ilustrar mediante el uso de los datos del
Ensayo de
Rendimiento de Cocina que se presentaron en la pagina
29.
Los ensayos a fuego abierto del nucleo
familiar, promediaron
[X.sub.1] =
3.56, [S.sub.1] = 0.644 y, [n.sub.1] = 6.
Los resultados para la estufa
tipo
"Kaya", X2 = 2.55, [S.sub.2] = 0.485 y, [n.sub.2] = 6.
El valor que
resulta de t
usando la ecuacion 6 es de 3.07. Ademas
existen
6 + 6 - 2 =
10 grados de libertad, pues las medias de cada grupo
han sido
calculados. Al usar la tabla puede
verse que el valor
de
"t" calculado es mayor que la cifra dada para un nivel de
significacion
del 1%, (2.76) pero que es menor para un nivel
de
significancia del 0.5% (3.17). Por lo
tanto existe menos
del 1% de
probabilidad de que el ahorro de lena obtenido se haya
debido a una
casualidad. Ademas, la ecuacion 11, nos
indica que
el intervalo
de confianza del 99% para el consumo especifico de
lena es de
1.01 [+ or -] (2.76 x0.108 x 3.055) = 1.01 [+ or -] 0.91 kg/comida.
Lo anterior significa
que existe un 99% de probabilidad de
ahorrar entre
0.10 y 1.92 kg/comida. Esto es
consistente con el
intervalo de
confianza del 95% que se calculo para la estufa
"Kaya"
y que, se discutio anteriormente.
Esta prueba
puede usarse tambien para comprobar la forma en que
factores no
controlados en los ensayos de cocinado y cocina
afectan la
economia de lena. Esto se hace
dividiendo la poblacion
del ensayo en
dos grupos, de acuerdo al factor de interes.
La division
puede hacerse juntamente con aspectos socio-economicos
(por ejemplo,
ingreso alto/bajo, tamano de familia, grande/
pequena) o
basarse en un factor relacionado con la cocina (por
ejemplo,
tamano de olla). Si se observa una
relacion significante
entre la
economia de lena y otros factores relacionados
con la
cocina, puede resultar apreciable estudiar a ese factor
en forma mas
sistematica usando el Ensayo del Agua Hirviendo.
Finalmente,
es posible reducir el consumo de lena incentivando
costumbres
que tengan correlacion con economias altas de lena
(y viceversa
en caso de costumbres ineficientes).
Seleccion del
Tamano de Muestra
El analisis
estadistico de los resultados del ensayo, puede resultar
edsx750.gif (600x600)


Previous File Next File